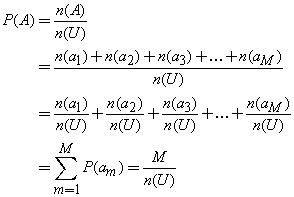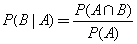Tony":2msxg389 said:
Lincolnshirebodger":2msxg389 said:
My links disagree.....................

If you have all 14 million tickets, each ticket has 1 in 14 million chance of winning ,but cumulatively you have 14 million in 14 million of winning, giving you a cumulative probability of 1.0
Dont confuse combinatorials with cumulative probabilities, its not the same thing.
Also, your maths is not correctly applied. You have to factorise the numbers.
The chance of winning the lottery, using 1 combination of 6 numbers out of 49 is:
(49!+48!+47!+46!.......2!+1) - (43!+42!+41!+....2!+1) to 1
Disagree all you want. The numbers I posted are correct. I carried out each of the calculations on a calculator and in excel using the inbuilt combin function (as a check) before posting!!!!
Don't believe all you read on the web.
I didn't use the web as I was taught stats 20+ years ago whilst studying for an engineering degree and have used it many times since .
The fact is that you have 50 chances, each of which is (just less than) 1 in 14 million to one. This is a statistical fact, not my opinion :roll: you do NOT have a 1 in 280000 chance of winning by doing this.
With the first ticket, you are using one of 13983816 chances to win.
With the second ticket, you are using 1 of 13983815 chances to win
With the 3rd ticket, you are using 1 of 13983814 chances to win
etc. etc.
Therefore, the chances of wining with 50 tickets are still just above "not a hope in hell"
If you toss a (balanced and fair) coin 20 times and it comes up heads each time, the probability of it coming up heads next time is still 1 in 2 or 0.5 regardless of the past history. The coin has no more chance of comig up heads agian than it did on the first toss.
No, sorry were going t ohave to agree to disagree. You clearly dont understand the principle of Cumulative Probability.
Take the coin. 50% chance of head or tail every time.
Thats not the same as saying 'whats the chance of throwing heads 10 times on the trot. Its two different measures.
The 1st Law of Probability:
The chances of something never happening: = 0
The chances of getting a head on one toss of a coin = 0.5
The chances of a the sun rising tomorrow = 1.0 (dead cert)
Events like coin tossing as you state are independant of one another. That however is not the same as predicting the odds for sequenced events - its an entirely separate situation.
Ive already pointed out (and no one as yet has addressed or rebutted the fact that if you own all 14 million lottery tickets then the chances of you winning is a dead cert, because you have 14 million chances at an odds of 14 million to one )
2nd Law of Probability:
The probability of two independent events both occurring is the product of there separate probabilities
3rd law of Probability:
The probability of anyone one of n mutually exclusive events occurring is the sum of there separate probabilities
These laws are attributed to
PROBABILITY THEORY: THE LOGIC OF SCIENCE
by
E. T. Jaynes
Wayman Crow Professor of Physics
Washington University
St. Louis, MO 63130, U.S.A.
so apply the above laws:
2 head in two throws: (law 2) 0.5 x 0.5 = 0.25
1 head and one tail in two throws = (law 3 ) 0.5 +0.5 = 1.0
4 heads in 4 throws - (law 2 ) 0.5 x 0.5 x 0.5 x 0.5 =0.0625
The chances of one lottery ticket winning = 1/14000000 = 7.14 x 10e-8
The chances of winning the lottery twice in two consecutive draws is law 2
7.14 x 10e-8 x 7.14 x 10e-8 = 5.15 x 10e-15
Conversely, the chances of winning one lottery draw with one of ten tickets
7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 + 7.14 x 10e-8 = 7.14 x 10e-7.
Cumulative Probability works exactly like that. The more different lottery tickets in the same draw you buy, the more chances you have of winning, its common sense, if nothing else.
To be precise and technical:
Join Probability: The probability of the desired outcomes is the sum of the probability of each event resulting in a desired outcome.
Suppose that the set of desired outcomes A has M different events, i.e., A={am|m=1,2,3,...,M}. The join probability indicates that :
Conditional Probability: Suppose that A and B are two sets of outcomes. The probability of B under the condition that A has happened, denoted by P(B|A), can be expressed as:
sorry about the heavy maths, but its the only way to prove the point.