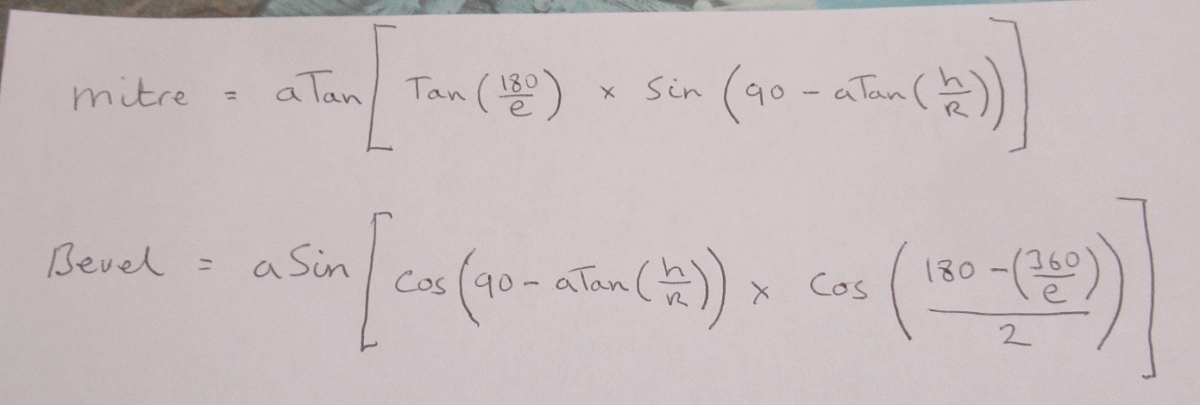Here's my drawing of the graphic setting out method, made it to fit my A4 scanner so smaller than our OP's design.
120mm square base, 100mm high, 20 mm thick timber, to make it easier to read and possibly to understand!
Would work similarly with different dimensions.
My drawing shows the square plan in pink and the plan of one of the triangular sides in pink, as though folded out flat.
In fact "folding out flat" is the key to the whole process in general
The green lines are the inner face and hence are the gauge lines for the bevels.
Transfer the lines to the workpiece and the pink and green triangles are all you need to make the thing; by hand working to the lines or by machine setting to cut bevels to meet the lines.
The only measurements put in are the base and height, all else is worked up on the drawing.
No need to measure any angles or even to know what they are as the workpieces are marked up with lines taken from the drawing, with dividers etc. and marking gauges. Two needed as there are two marking gauge settings
Quite easy to do but will confess it took a bit of revision - I thought there’d be an example in one of the books but they are all much more complicated!
I could attempt to explain how it’s done but I think this would be really difficult unless doing it live, so I’m not going to bother!
View attachment 152614
I've used the method several times as written up on my website
Making perfect trestles
I’ve made a few of these over the years, with variations, including a big brother of the lathe stand shown.
The setting out in the book (Joinery and Carpentry Vol 4 Greenhalgh, Richard (ed)) looks harder than it is, because it’s annotated all over, with construction lines and detailed explanations.
Once you’ve got the idea it goes quite easily with much less fuss.
What makes it hard to understand at first is that it would be easier to grasp as a set of 3 or 4 separate drawings, but in order to cross reference and avoid mistakes these are done over each other; developing the details from the plan and elevation put in first.
Hope that helps!