bugbear
Established Member
I've made a few staff and short staffs for a mate who's into martial arts.ED65":1fchute3 said:Just curious, does anyone here actually own a bokken, or a katana for that matter?
I used hickory.
BugBear

I've made a few staff and short staffs for a mate who's into martial arts.ED65":1fchute3 said:Just curious, does anyone here actually own a bokken, or a katana for that matter?
NazNomad":20f9xht5 said:Damn you and your ruler that can measure 0.038 of an inch. :-D
ED65":b6gngtqs said:Just curious, does anyone here actually own a bokken, or a katana for that matter?
MikeG.":3egji71r said:NazNomad":3egji71r said:Damn you and your ruler that can measure 0.038 of an inch. :-D
That's about half way between a 16th and a 32nd. The ruler can do that. My eyes can't do that any more if I forget to take my glasses out to the workshop.
MusicMan":1vhovgys said:Here's the maths IF and ONLY IF the curve you want is a circle. (If it isn't a circle, it is not defined).
the formula you want is
r^2 = a^2 + (r-s)^2
r is the radius of the circle
a is the half-length of the chord, 0.5 m in your case
s is the distance from the chord to the outside of the circle at the mid point, 0.02 m in your case.
Keith








bushwhaker":3tt1eydg said:Length the curve must be 110.35 cm.
Sheffield Tony":36zkf1jk said:The two right angled triangles have hypotenuse r, adjacent (r-s) and opposite a.
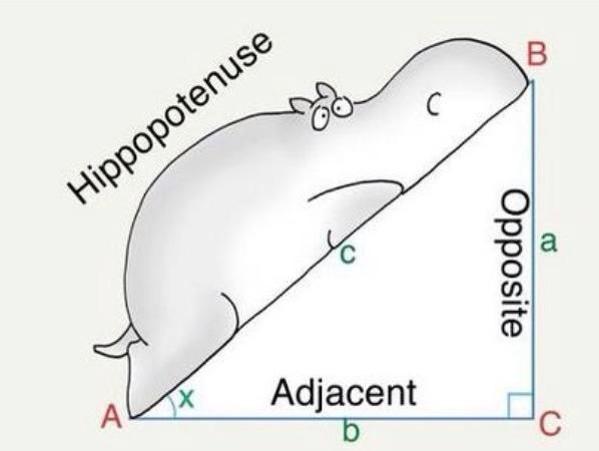
Measuring the sagitta for an existing arc is easy, as you say.Sheffield Tony":2dh5zory said:You don't really need to write this down. It is just Pythagoras theorem. Draw your arc, and the sector of the circle it forms part of. Draw a line bisecting the sector, and a straight line connecting the two end points of your arc. You now have a sort of kite shape with a rounded top. The two right angled triangles have hypotenuse r, adjacent (r-s) and opposite a.
Woody2Shoes":gmvm9kq7 said:Last time I used this was for copying an arch over a fireplace - easy to measure the span and the "rise" across that span, but hard to find the radius for the router jig.
Here's a nice website that shows you the maths and provides a calculator (the second one down) which matches MikeG's 6250 figure.
sunnybob":19t5n1l2 said:... It seems to have passed a lot of folks by, but my problem was solved on page two.
Just because you've finished with the thread, doesn't mean it can't continue so everyone learns something [WINKING FACE]sunnybob":jttc0j9d said:Hey, I've discovered perpetual motion.
It seems to have passed a lot of folks by, but my problem was solved on page two. ROFLMFAO.
Mea culpa!sunnybob":1palyu7i said:but my problem was solved on page two. ROFLMFAO.
Enter your email address to join: